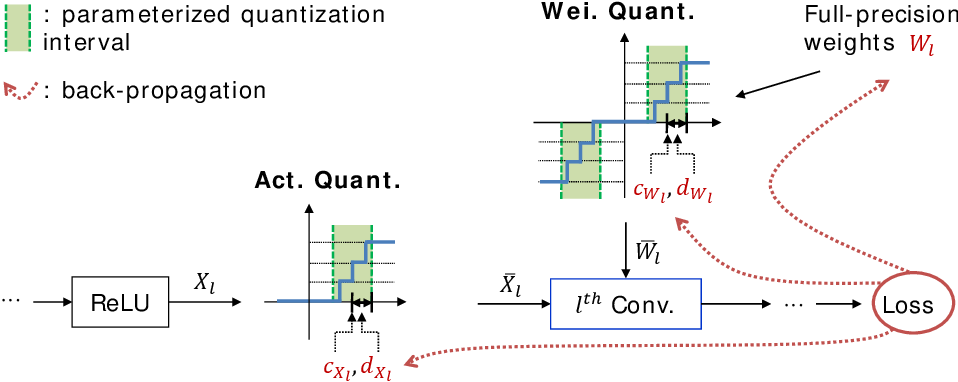
A Manual Implementation of Quantization in PyTorch - Single Layer

Introduction

The packaging of extremely complex techniques inside convenient wrappers in PyTorch often makes quick implementations fairly easy, it also removes the need to understand the inner workings of the code. However, this obfuscates the theory of why such things work and why they are important to us. For instance, for neither love or money, could I figure out what a QuantStub and a DeQuant Stub really do and how to replicate that using pen and paper. In embedded systems one often has to code up certain things from scratch, as it were and sometimes PyTorch’s “convenience” can be a major impediment to understanding the underlying theory. In the code below, I will show you how to quantize a single layer of a neural network using PyTorch. And explain each step in excruciating detail. At the end of this article you will be able to implement quantization in PyTorch (or indeed any other library) but crucially, you will be able to do it without using any quantize layers, you can essentially use the usual “vanilla” layers. But before that we need to understand how or why quantization is important.

Quantization

The process of quantization is the process of reducing the number of bits that represent a number. This usually means we want to use an integer instead of a real number, that is, you want to go from using a floating point number to an integer. It is important to note that the reason for this is because of the way we multiply numbers in embedded systems. This has to do with both the physics and the chemistry of a half-adder and a full adder. It just takes longer to multiply two floats together than it does to multiply two integers together. For instance, multiplying is a much more complex operation than multiplying . So it is not simply a consequence of reducing the “size” of the number. In the future, I will write a blog post about why physics has a lot to do with why this is.

Outline

I start with the intuition behind Quantization using a helpful example. And then I outline a manual implementation of quantization in PyTorch. So what exactly does “manual” mean?

1. I will take a given, assumed pre-trained, PyTorch model (1 Fully connected layer with no bias) that has been quantized using PyTorch’s quantization API.
2. I will extract the weights of the layer and quantize them manually using the scale and zero point from the PyTorch quantization API.
3. I will quantize the input to the layer manually, using the same scale and zero point as the PyTorch quantization API.
4. I will construct a “vanilla” fully connected layer (as opposed to the quantized layer in step 1) and multiply the quantized weights and input to get the output.
5. I will compare the output of the quantized layer from step 1 with the output of the “vanilla” layer from step 4.

This will inherently allow you to understand the following :

1. How to quantize a layer in PyTorch and what quantizing in PyTorch really means.
2. Some potentially confusing issues about what is being quantized, how and why.
3. What does the QuantStub and DeQuantStub really do and how to replicate that using pen and paper.

At the end of this article you should be able to :

1. Understand Quantization conceptually.
2. Understand PyTorch’s quantization API.
3. Implement quantization manually in PyTorch.
4. Implement a Quantized Neural Network in PyTorch without using PyTorch’s quantization API.

Intuition behind Quantization

The best way to think about quantization is to think of it through an example. Let’s say you own a store, and you are printing labels for the prices of objects, but you want to economize on the number of labels you print. Assume here for simplicity that you can print a label that shows a price lower than the price of the product but not more. If you print tags for 0.20 cents, you get the following table, which shows a loss of 0.97 by printing 6 labels. This obviously didn’t save you much as you might as well have printed labels with the original prices and lost in sales.

Price	Tags	Loss
1.99	1.8	-0.19
2.00	2	0.00
0.59	0.4	-0.19
12.30	12	-0.30
8.50	8.4	-0.10
8.99	8.8	-0.19
	6	-0.97

Maybe we can be more aggressive, by choosing tags rounded to the nearest dollar instead, we can obviously lose more money but we save on one whole tag!

Price	Tags	Loss
1.99	1	-0.99
2.00	2	0.00
0.59	0	-0.59
12.30	12	-0.30
8.50	8	-0.50
8.99	8	-0.99
	5	-3.37

How about an even more aggressive one? We round to the nearest dollars and use just two tags. But then we are stuck with a massive loss of dollars.

Price	Tags	Loss
1.99	0	-1.99
2.00	0	-2.00
0.59	0	-0.59
12.30	10	-2.30
8.50	0	-8.50
8.99	0	-8.99
	2	-24.37

In this example, the price tags represent memory units and each price tag printed costs a certain amount of memory. Obviously, printing as many price tags as there are goods results in no loss of money but also the worst possible outcome as far as memory is concerned. Going the other way reducing the number of tags results in the largest loss in money.

Quantization as an (Unbounded) Optimization Problem

Clearly, this calls for an optimization problem, so we can set up the following one : let be the quantization function , then the loss is as follows,

Where is a count of the unique values that over the entire interval of, .

Issues with finding a solution

A popular assumption is to assume that the function is a rounding of a linear transformation. The constraint that minimizes is difficult since the function is unbounded. We could solve this if we knew at least two points at which we knew the expected output for the quantization problem, but we do not, since there is no bound on the highest tag we can print. If we could impose a bound on the problem, we could evaluate the function at the two bounds and solve it. Thus setting a bound seems to solve both problems.

Quantization as Bounded Optimization Problem

In the previous section, our goal was to reduce the number of price tags we print, but it was not a bounded problem. In your average grocery story prices could run between dollars and a dollars. Using the scheme above you could certainly print fewer labels. But you could also end up printing a large number of labels in absolute terms. You could do one better by pre-determining the number of labels you want to print. Let us then, set some bounds on the number of labels we want to print, consider the labels you want to print as , this is fairly aggressive. Again we can set up the optimization problem as follows (there is no need to minimze , the count of unique labels for now, since we are defining that ourselves), where is the scale and is the zero point. It must be true that, Evaluating the above equations gives us the general solution This gives us the solution, .

Price	Label	Loss
1.99	0	-1.99
2	0	-2
0.59	-1	-1.59
12.3	2	-10.3
8.5	1	-7.5
8.99	1	-7.99
	4	-31.37

This gives the oft quoted quantization formula, Similarly, we get reverse the formula to get the dequantization formula i.e. starting from a quantized value we can guess what the original value must have been, This is obviously lossy.

Implication of Quantization

We have shown that given some prices, we can quantize them to a smaller set of labels. Thus saving on the cost of labels. What if you remembered and and then you used the dequantization formula to guess what the original price was and charge the customer that amount? This way you can save on the number of labels, but you can get closer to the original price by just writing down and and using the dequantization formula. We can actually do a better job with prices as well as saving on the number of labels. However, this is lossy, and you will lose some money. In this example, we notice that we consider charging more or less than the actual price as a loss both ways, to keep things simple.

Price	Label	Loss	DeQuant	De-q loss
1.99	0	1.99	3.90	1.91
2.00	0	2.00	3.90	1.90
0.59	-1	1.59	0.00	0.59
12.30	2	10.3	11.71	0.59
8.50	1	7.50	7.80	0.69
8.99	1	7.99	7.80	1.18
	4	31.37		6.87

Quantization of Matrix Multiplication

Using this we can create a recipe for quantization to help us in the case of neural networks. Recall that the basic unit of a neural network is the operation,

We can apply quantization to the weights and the input (). We can then use dequantization to get the output.

Our goal of trying to avoid the floating point multiplication between can now be achieved by replacing them with their respective quantized values and scaling and subtracting the zero point to get the final output. Here, and are quantized matrices and thus the multiplication operation (after multiplying it out) is now not between two floating point matrices and but between and . Which are both integer matrices. This allows us to save on memory and computation since it is cheaper to multiply integers together than it is to multiple floats. However, in practice since, are also integers, is also an integer multiplication, so we just use that mulitplication instead of multiplying out the whole thing.

Code

Consider the following original,

class M(torch.nn.Module):
    def __init__(self):
        super(M, self).__init__()
        # QuantStub converts tensors from floating point to quantized
        self.quant = torch.quantization.QuantStub()
        self.fc = torch.nn.Linear(2, 2, bias=False)
        # DeQuantStub converts tensors from quantized to floating point
        self.dequant = torch.quantization.DeQuantStub()

    def forward(self, X):
        # manually specify where tensors will be converted from floating
        # point to quantized in the quantized model
        X = self.quant(X)
        x = self.fc(X) # [[124.,  36.]
        # manually specify where tensors will be converted from quantized
        # to floating point in the quantized model
        x = self.dequant(x)
        return x

Now consider, the manual quantization of the weights and the input. model_int8 represents the quantized model. The QuantM2 class is the manual quantization of the model. The prepare_model function uses PyTorch convenience functions for quantization of the weights and the input i.e. get , from this model and compute the other steps. You can calculate these yourself as well, using the distributions of the input data and activation functions. The quantize_tensor_unsigned function is the manual quantization of the input tensor. The pytorch_result function is that computes the output of the fully connected layer of the PyTorch quantized model. The forward function is the manual quantization of the forward pass of the model.

def prepare_model(model_fp32, input_fp32):
    # model must be set to eval mode for static quantization logic to work
    model_fp32.eval()
    model_fp32.qconfig = torch.quantization.QConfig(
        activation=MinMaxObserver.with_args(dtype=torch.quint8),
        weight=MinMaxObserver.with_args(dtype=torch.qint8)
    )
    # Prepare the model for static quantization. This inserts observers in
    # the model that will observe activation tensors during calibration.
    model_fp32_prepared = torch.quantization.prepare(model_fp32)
    model_fp32_prepared(input_fp32)

    model_int8 = torch.quantization.convert(model_fp32_prepared)
    return model_int8


def quantize_tensor_unsigned(x, scale, zero_point, num_bits=8):
    # This function mocks the PyTorch QuantStub function which quantizes the input tensor
    qmin = 0.
    qmax = 2. ** num_bits - 1.

    q_x = zero_point + x / scale
    q_x.clamp_(qmin, qmax).round_()
    q_x = q_x.round().byte()

    return QTensor(tensor=q_x, scale=scale, zero_point=zero_point)
    
class QuantM2(torch.nn.Module):

    def __init__(self, model_fp32, input_fp32):
        super(QuantM2, self).__init__()
        self.fc = torch.nn.Linear(2, 2, bias=False)
        self.model_int8 = prepare_model(model_fp32, input_fp32)
        # PyTorch automatically quantizes the model for you, we will use those weights to compute a forward pass
        W_q = self.model_int8.fc.weight().int_repr().double() 
        z_w = self.model_int8.fc.weight().q_zero_point()
        self.fc.weight.data = (W_q - z_w)

    @staticmethod
    def pytorch_result(model_int8, input_fp32):
        pytorch_res = model_int8.fc(model_int8.quant(input_fp32)).int_repr().float()
        return pytorch_res

    def forward(self, x):
            input_fp32 = x
            s_x = self.model_int8.quant(input_fp32).q_scale()
            z_x = self.model_int8.quant(input_fp32).q_zero_point()
            quant_input_unsigned = quantize_tensor_unsigned(input_fp32, s_x,z_x)
            z_x = quant_input_unsigned.zero_point
            s_x = quant_input_unsigned.scale
            s_w = self.model_int8.fc.weight().q_scale()
            x1 = self.fc(quant_input_unsigned.tensor.double() - z_x)
            # this next step is equivalent to dequantizing the output of the fully connected layer
            # it not exactly equivalent since I already subtracted the two zero points
            # you can derive a much longer quantization formula that multiplies W_q * X_q and has additional terms
            # you can then put W_q in the fc layer and X_q in the forward pass
            # and then use all those additional terms in the below step to requantize
            # in embedded systems its easy to use the formulation here
            x1 = x1 * (s_x * s_w)
            return x1

Sample run code of the above code is as follows,

cal_dat = torch.randn(1, 2)
model = M()
# graph mode implementation
sample_data = torch.randn(1, 2)
model(sample_data)
quant_model= QuantM2(model_fp32=model, input_fp32=sample_data)
quant_model(sample_data)
quant_model.model_int8(sample_data) # this is the quantized model, M2 should match it exactly, M is the original non quantized model. For small data sets there is usually no divergence.
# but in practice, the quantized model will be faster and use less memory, but will lose some accuracy

Let us start by analyzing the output of a quant layer of our simple model. The output of the int_models quantized layer is (somewhat counter-intuitively) always a float, this does not mean it is not quantized, it simply means you are shown the non-quantized value. If you look at the output, you will notice, it has dtype, quantization_scheme, scale and zero_point. You can view the value that will actually be used when it is called within the context of a quant layer by calling its int representation.

#recreate quant layer
int_model = quant_model.model_int8
default_pytorch_quant_layer_output = int_model.quant(sample_data)
# OUTPUT
# tensor([[0.1916, 0.5428]], size=(1, 2), dtype=torch.quint8,
#        quantization_scheme=torch.per_tensor_affine, scale=0.0021285151597112417,
#        zero_point=0)

actual_pytorch_quant_layer_output = int_model.quant(sample_data).int_repr()
# OUTPUT
# tensor([[90, 255]], dtype=torch.uint8)

Our manual quantization layer is a bit different, it outputs a QTensor object, which contains the tensor, the scale and the zero point. We get the scale and the zero point from the PyTorch quantized model’s quant layer (again, we could easily have done this by ourselves using the sample data).

manual_quant_layer_output = quantize_tensor_unsigned(sample_data, int_model.quant(sample_data).q_scale(), int_model.quant(sample_data).q_zero_point())
# OUTPUT
# QTensor(tensor=tensor([[ 90, 255]], dtype=torch.uint8), scale=0.0021285151597112417, zero_point=0)

Now let us look at the output of the quant layer AND the fully connected layer.

#recreate the fully connected layer operation
pytorch_fc_quant_layer_output = int_model.dequant(int_model.fc(int_model.quant(sample_data)))
# tensor([[-0.7907,  0.6919]])
manual_fc_quant_layer_output = quant_model(sample_data)
# tensor([[-0.7886,  0.6932]], dtype=torch.float64, grad_fn=<MulBackward0>)

It is worthwhile to point out a few things. First, the following two commands seem to give the same values but are very different. The first is a complete tensor object that gives float values but is actually quantized, look at dtype, it is actually quint.8.

int_model.fc(int_model.quant(sample_data))
# tensor([[-0.7907,  0.6919]], size=(1, 2), dtype=torch.quint8,
#        quantization_scheme=torch.per_tensor_affine, scale=0.0058139534667134285,
#        zero_point=136)

The output of this is a truly a float tensor, it not only shows as float values (same as before) but contains no quantization information.

int_model.dequant(int_model.fc(int_model.quant(sample_data)))
 # tensor([[-0.7907,  0.6919]])

Thus, in order to recreate a quantization operation from PyTorch in any embedded system you do not need to implement a de-quant layer. You can simply multiply and subtract zero points from your weight layers appropriately. Look for the long note inside the forward pass of the manually quantized model for more information.

A Word on PyTorch and Quantization

PyTorch’s display in the console is not always indicative of what is happening in the back end, this section should clear up some questions, you may have (since I had them). The fundamental unit of data that goes between layers in PyTorch is always a Tensor, that is always displayed as a float. This is fairly confusing since when we think of a vector/tensor as quantized we see all the data as integers. But PyTorch works differently, when a tensor is quantized it is still displayed as a float, but its quantized data type and quantization scheme to get to that data type is stored as additional attributes to the tensor object. Thus, do not be confused if you still see float values displayed, you must look at the dtype to get a clear understanding of what the values are. In order to view a quantized tensor as a int, you need to call int_repr() on the tensor object. Note, this throws an error if the tensor has not been quantized in the first place. Also, note that when PyTorch encounters a quantized tensor, it will carry out multiplication on the quantized values automatically and thus the benefits of quantization will be realized even if you do not actually see them. When exporting the model this information is packaged as well, no need for anything extra to be done.

A Word on Quant and DeQuant Stubs

This is perhaps the most confusing of all things about quantization in PyTorch, the QuantStub and DeQuantStub.

1. The job of de-quantizing something is automatically taken care of by the previous layer, as mentioned above. Thus when you come to a DeQuant Layer all it seems to do is just strip away the memory of having ever been quantized and ensures that the floating point representation is used. That is what is meant by the statement “DeQuantStub is stateless”, it literally needs nothing to function, all the information it needs to function will be packaged with the input tensor you feed into it.
2. The Quant Stub, on the other hand, is stateful it needs to know the scale and the zero point of what is being fed into it, and the network has no knowledge of the input data, which is why you need to feed data into the Neural Network to get this going, if you knew the scale and zero point of your data already you could directly input that information into the QuantStub.
3. The QuantStub and DeQuantStub are not actually layers, they are just functions that are called when the model is quantized.
4. Another huge misconception is when and where to call these layers, every example on the PyTorch repo will have the Quant and DeQuant stub sandwiching the entire network, this leads people to think that the entire network is quantized. This is not true see the following section for more information.

Do you need to insert a Quant and DeQuant Stub after every layer in your model?

Unless you know exactly what you are doing, then YES you do. In most cases, especially for first time users, you usually want to dequantize immediately after quantizing. If you want to “quantize” every multiplication operation but dequantize the result (i.e. try to bring it back to your original scale of data) then yes, you do. The Quant and DeQuant Stub is “dumb” in the sense that it does not know what the previous layer was, if you feed it a quantized tensor it dequantizes it. It has no view of your network as a whole and does not modify the behavior of the network as a whole. Recall the mathematics of what we are trying to do. We want to replace a matrix multiplication, with . Now what if you want to replace this across multiple layers i.e. you want to quantize the following expression :

Your first layer weights are and the second layer weights are . You want to quantize the entire expression. Ask yourself what do you really want to do, in most cases what you really want to do, is quantize the two matrix multiplies, you inevitably have to do, so that they do not occur in float representation but rather occur in integer. This means you want to replace with and thus replacing the whole expression with . If you do not dequantize after every layer you will end up executing the following equation, as the entire first layer will be quantized, its output will be recorded and then that quantized value in int8 will flow to the next layer. After this, all the quantization information will be lost i.e. the scale and zero point will be lost. The DeQuant layer will simply use the information from the previous layer to dequantize the output, so only the most recent layers output will be dequantized.

When do you not need to put Quant and DeQuant Stubs after every layer?

Dequantizing comes with a cost, you need to compute floating point multiplications, in order to multiply the weights with the matrix. This is certainly less than the floating point operations from the original matrix multiplication itself (a lot less than storing the output from another whole floating point matrix), but it is still a lot. However, in many of my use cases, I could get away with not dequantizing. While the real reasons are still not clear to me (like most things in neural networks), I would guess that for some of my layers the weights were not that important to getting my overall accuracy. I was also in the Quantize Aware Framework, maybe I will do a post about this too.

Conclusion

In this blog post we covered some important details about PyTorch’s implementation of quantization that are not immediately obvious. We then went on to manually implement a quantized layer and a quantized model. We then showed how to use the quantized layer and the quantized model to get the same results as the PyTorch quantized model. We also showed that the PyTorch quantized model is not actually quantized in the sense that the values are integers, but that the values are quantized in the sense that the values are stored as tensor objects (that store their quantization parameters with them) and the operations are carried out on the integers. This is a very important distinction to make. Additionally, in inference mode, you can just take out the quantized weights, and skip the fc layer step as well, you can just multiply the two matrices together. This is what I will be doing in the embedded system case. In my next posts, I will show you how to quantize a model and the physics behind why multiplying two floats is more expensive than multiplying a two integers.