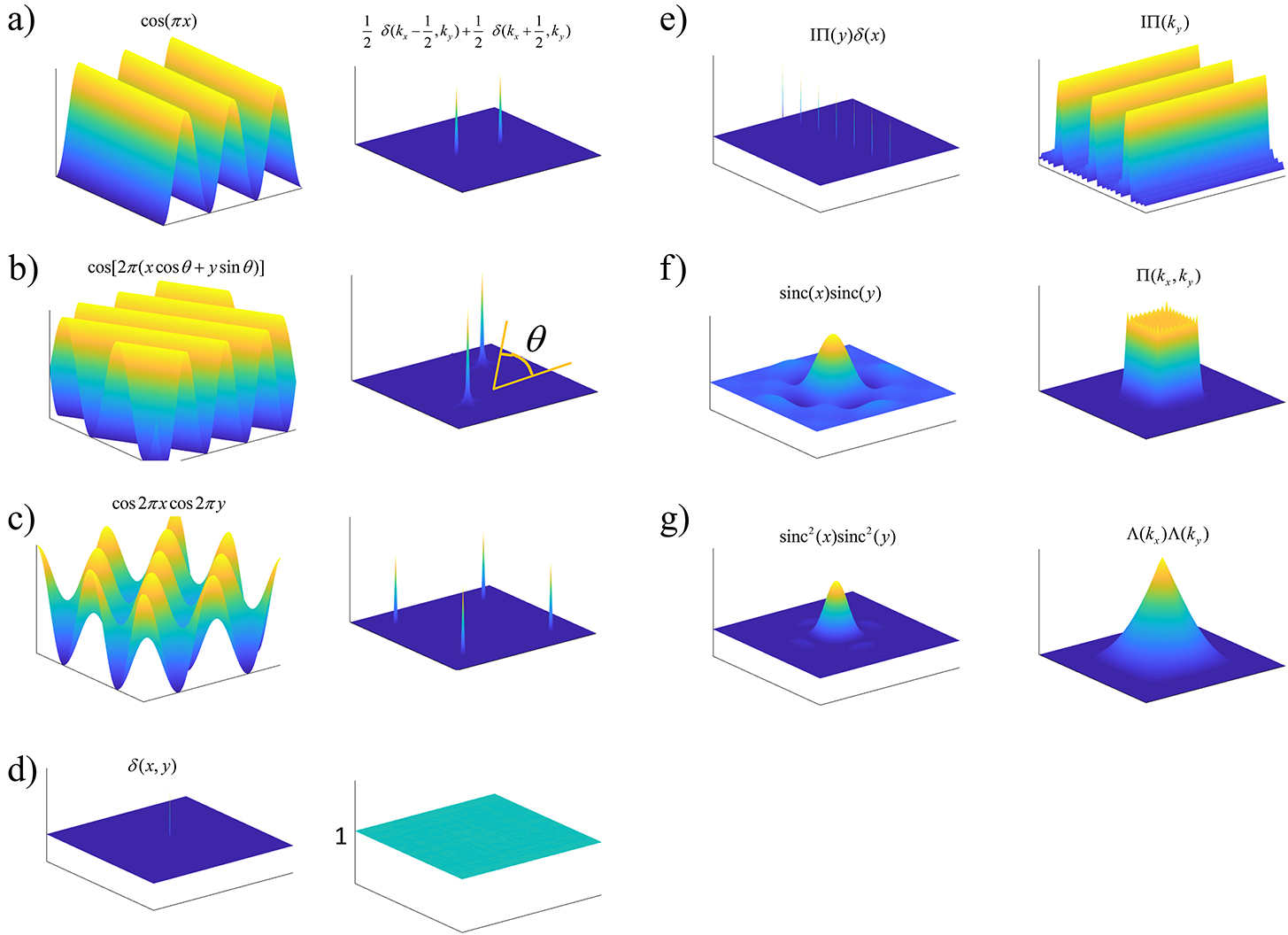
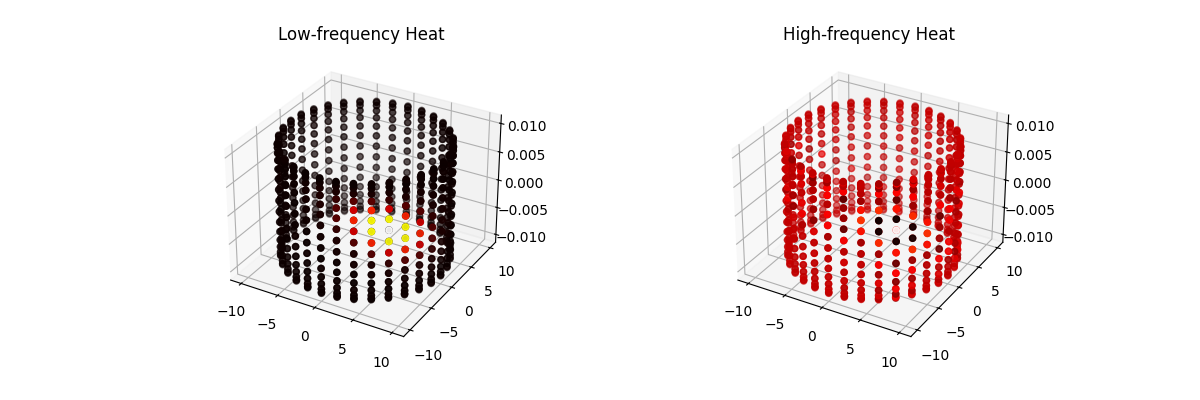
Locality, Learning, and the FFT: Why CNNs Avoid the Fourier Domain
Explore how Fourier transforms on graphs power spectral GCNs, from modeling heat flow to solving cold-start recommendations.
Read moreA review of the mathematical essentials for recommender systems, comparing matrix factorization and graph neural networks.
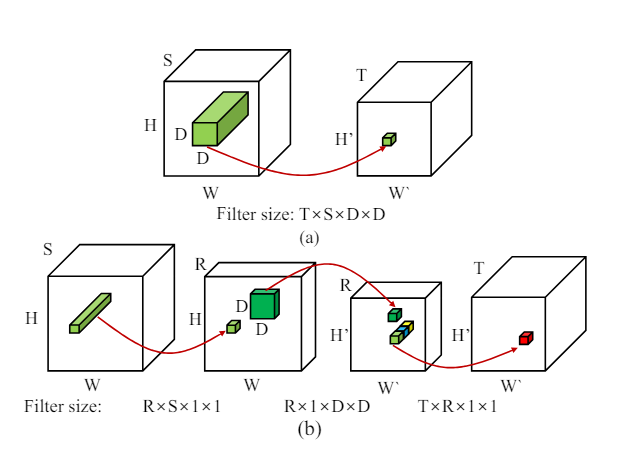
Read morePart III : What does Low Rank Factorization of a Convolutional Layer really do?
In this post, we will explore the Low Rank Approximation (LoRA) technique for shrinking neural networks for embedded systems. We will focus on the Convolutional Neural Network (CNN) case and discuss the rank selection process.
Read morePart II : Shrinking Neural Networks for Embedded Systems Using Low Rank Approximations (LoRA)
In this post, we will explore the Low Rank Approximation (LoRA) technique for shrinking neural networks for embedded systems. We will focus on the Convolutional Neural Network (CNN) case and discuss the rank selection process.
Read more