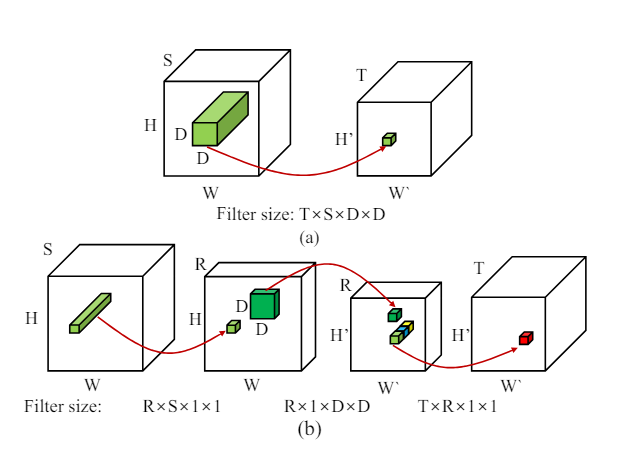
Part III : What does Low Rank Factorization of a Convolutional Layer really do?
In this post, we will explore the Low Rank Approximation (LoRA) technique for shrinking neural networks for embedded systems. We will focus on the Convolutional Neural Network (CNN) case and discuss the rank selection process.
Read more