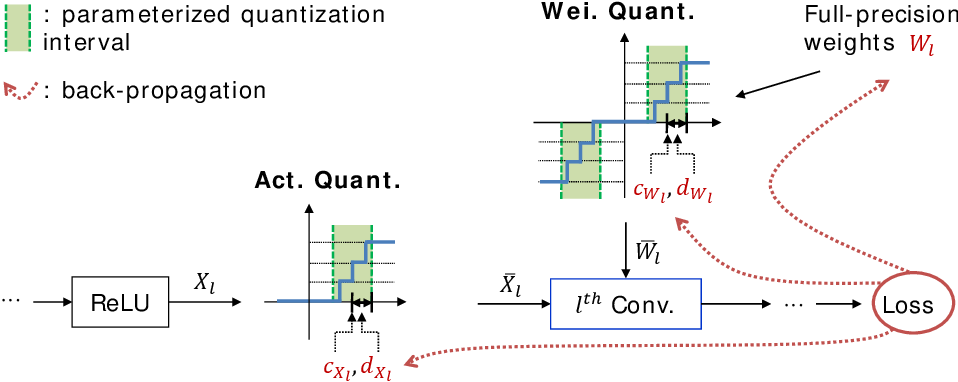
Are Values Passed Between Layers Float or Int in PyTorch Post Quantization?
In this article, we will discuss how values are passed between layers post quantization in PyTorch. We will also discuss why floating point operations are slower than integer operations.
Read more